Equidistributed sequence
In mathematics, a bounded sequence {s1, s2, s3, …} of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that interval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration.
Contents |
Definition
A bounded sequence {s1, s2, s3, …} of real numbers is said to be equidistributed on an interval [a, b] if for any subinterval [c, d] of [a, b] we have
(Here, the notation |{s1,…,sn }∩[c,d]| denotes the number of elements, out of the first n elements of the sequence, that are between c and d.)
For example, if a sequence is equidistributed in [0, 2], since the interval [0.5, 0.9] occupies 1/5 of the length of the interval [0, 2], as n becomes large, the proportion of the first n members of the sequence which fall between 0.5 and 0.9 must approach 1/5. Loosely speaking, one could say that each member of the sequence is equally likely to fall anywhere in its range. However, this is not to say that {sn} is a sequence of random variables; rather, it is a determinate sequence of real numbers.
Discrepancy
We define the discrepancy D(N) for a sequence {s1, s2, s3, …} with respect to the interval [a, b] as
A sequence is thus equidistributed if the discrepancy D(N) tends to zero as N tends to infinity.
Equidistribution is a rather weak criterion to express the fact that a sequence fills the segment leaving no gaps. For example, the drawings of a random variable uniform over a segment will be equidistributed in the segment, but there will be large gaps compared to a sequence which first enumerates multiples of ε in the segment, for some small ε, in an appropriately chosen way, and then continues to do this for smaller and smaller values of ε. See low-discrepancy sequence for stronger criteria and constructions of low-discrepancy sequences for constructions of sequences which are more evenly distributed.
Equidistribution modulo 1
The sequence {a1, a2, a3, …} is said to be equidistributed modulo 1 or uniformly distributed modulo 1 if the sequence of the fractional parts of the an's, (denoted by an−⌊an⌋)
is equidistributed in the interval [0, 1].
Examples
- The sequence of all multiples of an irrational α,
-
- 0, α, 2α, 3α, 4α, …
is uniformly distributed modulo 1: this is the equidistribution theorem.
- More generally, if p is a polynomial with at least one irrational coefficient (other than the constant term) then the sequence p(n) is uniformly distributed modulo 1: this was proved by Weyl and is an application of the theorem of Johannes van der Corput.
- The sequence log(n) is not uniformly distributed modulo 1.
- The sequence of all multiples of an irrational α by successive prime numbers,
-
- 2α, 3α, 5α, 7α, 11α, …
is equidistributed modulo 1. This is a famous theorem of analytic number theory, proved by I. M. Vinogradov in 1935.
- The van der Corput sequence is equidistributed.
Properties
The following three conditions are equivalent:
- {an} is equidistributed modulo 1.
- For every Riemann integrable function f on [0, 1],
- For every nonzero integer k,
-
The third condition is known as Weyl's criterion. Together with the formula for the sum of a finite geometric series, the equivalence of the first and third conditions furnishes an immediate proof of the equidistribution theorem.
Metric theorems
Metric theorems describe the behaviour of a parametrised sequence for almost all values of some parameter α: that is, for values of α not lying in some exceptional set of Lebesgue measure zero.
- For any sequence of distinct integers bn, the sequence {bn α} is equidistributed mod 1 for almost all values of α.[1]
- The sequence {αn} is equidistributed mod 1 for almost all values of α > 1.[2]
It is not known whether the sequences {en} or {πn} are equidistributed mod 1. However it is known that the sequence {αn} is not equidistributed mod 1 if α is a PV number.
Well-distributed sequence
A bounded sequence {s1, s2, s3, …} of real numbers is said to be well-distributed on [a, b] if for any subinterval [c, d] of [a, b] we have
uniformly in k. Clearly every well-distributed sequence is uniformly distributed, but the converse does not hold. The definition of well-distributed modulo 1 is analogous.
See also
References
- ^ See Satz 1, Über eine Anwendung der Mengenlehre auf ein aus der Theorie der säkularen Störungen herrührendes Problem, Felix Bernstein, Mathematische Annalen 71, #3 (September 1911), pp. 417-439, doi:10.1007/BF01456856.
- ^ Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins, J. F. Koksma, Compositio Mathematica, 2 (1935), pp. 250-258.
- L. Kuipers; H. Niederreiter (2006). Uniform Distribution of Sequences. Dover Publishing. ISBN 0-486-45019-8.
- L. Kuipers; H. Niederreiter (1974). Uniform Distribution of Sequences. John Wiley & Sons Inc.. ISBN 0-471-51045-9.
![\lim_{n\to\infty}{ \left|\{\,s_1,\dots,s_n \,\} \cap [c,d] \right| \over n}={d-c \over b-a} . \,](/2012-wikipedia_en_all_nopic_01_2012/I/cefbaaedc02643bfe0c760249c43753e.png)
![D(N) = \sup_{a\le c\le d\le b} \left\vert \frac{\left|\{\,s_1,\dots,s_N \,\} \cap [c,d] \right|}{N} - \frac{d-c}{b-a} \right\vert . \,](/2012-wikipedia_en_all_nopic_01_2012/I/8c1680471d1f664a363d93b46af0be01.png)
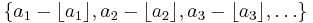
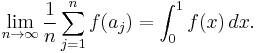
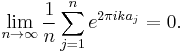
![\lim_{n\to\infty}{ \left|\{\,s_{k%2B1},\dots,s_{k%2Bn} \,\} \cap [c,d] \right| \over n}={d-c \over b-a} \,](/2012-wikipedia_en_all_nopic_01_2012/I/95cdac6073216610e334abc71cfe53ca.png)